这记录一些我刚开始学习所用到的数学

 

基础从最基础的开始

小知识：

　　0 ∈ ｛0 1

｛0 1｝表示一个集合，里面有0,1两个元素。所以0属于这个集合，就用0 ∈ ｛0 1｝表示了。∈代表属于。 ｛0  ｝ ∈ ｛0   1｝是错误的，一个集合不能属于另一个集合。 反着的E:谓词逻辑  存在量词 ∃ x:P(x) 意味着有至少一个 x 使 P(x) 为真.n ∈ N:n 是偶数. 倒着的A:存在着  全称量词 ∀ x:P(x) 意味着所有的 x 都使 P(x) 都为真.n ∈ N:n2 ≥ n. 对于所有；对于任何；对于每个  谓词逻辑  ∧ 逻辑合取 陈述 A ∧ B 为真,如果 A 与 B 二者都为真；否则为假.n < 4 ∧ n >2 ⇔ n = 3 当 n 是自然数的时候. 与  命题逻辑  ∨ 逻辑析取 陈述 A ∨ B 为真,如果 A 或 B (或二者)为真；如果二者都为假,则陈述为假.n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 当 n 是自然数的时候. 或  命题逻辑

一 标量,向量,矩阵,张量

(1)标量:

　　标量在计算机学习中我认为可以理解成,一个用于统计或者标记这一类行数学事件当中一个值得标志,比方说,当它表示一条线的斜率的时候,他只有这么一个用处,而且也只是需要这么一个而已,他不需要再有别的定义,只代表斜率只有一个值就可以了. 在比方说,一个数组中我们可以定义一个标量,这个标量就是这个数组的数量.所以我理解标量像是一道数学题中唯一的答案.  就好比 标量等于答案 标量的值等于结果. 如果这道题 出现了变化,那么这个标量就不是原来的那个标量.

　　展现方式:

　　　　表达一条线的斜率: 令s ∈ R 表示一条线的斜率’

　　　　表达数组的数量 :    令n ∈ N 表示元素的数目

(2)向量:

　　一个向量代表一列数，这些数求有序排列，我们可以按照索引的序列确定每个单独的书，通常用小写的粗体来表示，比如x。向量中的元素可以通过带角标的斜体表示，向量x的第一个元素是x₁，那么第二个元素就是x₂，以此类推。如果每个元素都属于标量R,并且该向量有n个元素，那么该向量属于实属集R的n次笛卡尔乘积的集合，当需要明确表示向量中的元素时，我们将元素排列成一个方括号包围的纵列

 

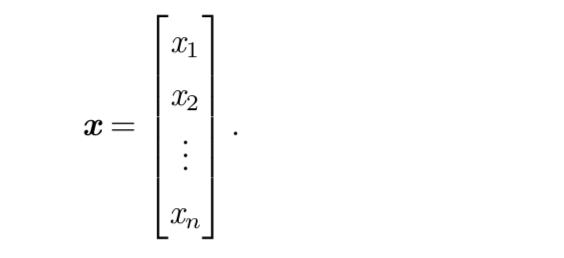
我们可以把向量看作空间重的点，每个元素使不同的坐标轴上的坐标， （但是我怎么看他们都可连接成一条线啊，奇了怪了）

有时候我们需要索引向量中的一些元素。在这种情况下，我们定义一个包含这些元素的索引集合，然后将该集合写在脚标处。比如，指定x1，x3和x₆，我们定义集合s={1,3,6}，然后写作x_{s。我们用符_表示集合的补集中的索引。（补集就是补充满所需要的其他的啦，这个不算的啦）} 比如x_₁ 表示x中除了x1意外的所有元素，x_{_s}表示x中除了x₁，x₃和x₆外所有的元素构成的向量。这就很有意思了同时也很好理解了。我们要在这个向量中 取出不包含的剩下的部分，那我们干脆吧 _ 当作减号 减去他就可以了

（3）矩阵：

　　矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个），可以认为 两个向量像拉锁一样拼在一起。只有两两结合才能算作一个整体，当然了矩阵也不代表着一定是两列。可以是好几列。通常赋予矩阵粗体大写的变量名称，比方说A。如果一个实数矩阵高度为m，宽度为n 那么我们说A ∈ R^mxn 。我们在表示矩阵中的元素时。通常以不加粗的斜体形式使其用名称，索引用逗号间隔。比如，A_1，1表示在矩阵A中左上角的那个元素，A_m,n表示A右下的元素。我们通过用：表示要用到一排了或者一列了。比方说A_m,:表示我要使用m行所有的元素。

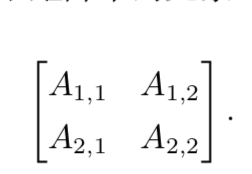
有时我们需要矩阵值表达式的索引，而不是单个元素。在这种情况下，我们在表达式后面接下标，但不必将矩阵的变量名称小写话。 （就是 我想给 i行j列的这个元素函数求值，这时候我们的这个a可以大写成A） 比如f（A）_i,j 这么写，表示函数f（）作用在A上的矩阵的第i行j列元素上

(4)张量:

　　如果说矩阵式二维的数组,那么 张量就相当于在维上加维一下, 如果一般情况下,一个数组中的元素分布在若干维坐标的规则网格中,我们称之为张量. 通常用A来表示张量"A". 张量A中坐标为(i,j,k)的元素记做A_{i,j,k  .}